TI-Nspire Family

TI-NspireCX Summary

Calculator 1

 (CXとCX CASの違い）

Calculator 2

　(数値計算）

Calculator 3

　(数式処理）

Calculator 4

　(数式処理・大学）

Calculator 5

　(メニュー）

Graph 1

　(描けるグラフ）

Graph 2

　(動かす）

Graph 3

　(視覚化の有効性）

Geometry 1

 （作図例，+Graph）

 （メニュー）

Spreadsheet/Stat 1

 (統計・概要とメニュー)

Spreadsheet/Stat 2

  （統計・プロット）

DataQust 1

  （データ収集）

DataQust 2

  （センサー）

Docking Station for CX

Software Summary

Student Software

Teacher Software

教材データベース

ここをクリックすると画面の動きをみることができます。

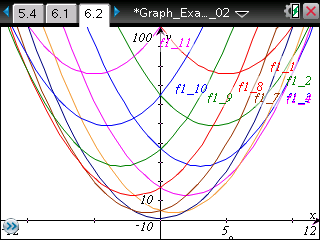
aに具体的な値を入れてグラフを描いてみます。

求める領域は，放物線y＝x²が軸をy軸に平行のまま，

頂点がy＝3x²＋1上を動いてできたものです。

　　TI-Nspire CX

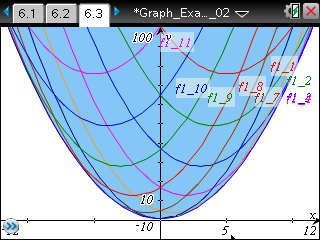
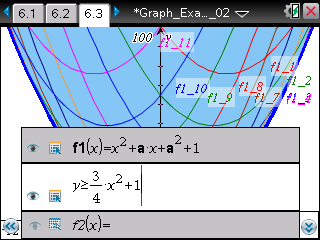
aについて整理した2次式の実数条件から点（x, y）の

存在範囲を求めると，判別式≧0 より，

が求める範囲です。

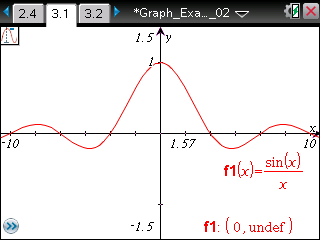
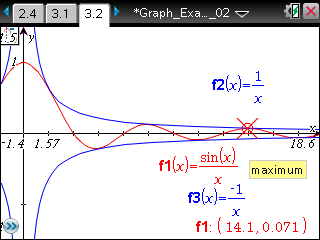
グラフをトレースします。

x＝0のとき，yの値がないことに留意します。

トレースを続けるとプラス・マイナスを繰り返しながらx軸に

近づいていく様子が見えます。

y＝1/xとy＝−1/xのグラフをいっしょに描くと，

これがいつもの授業で代数的に解いている

「はさみうちの原理」の視覚化です。

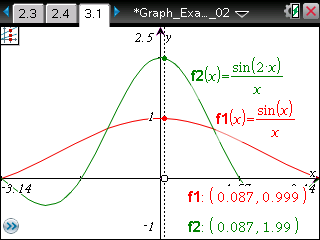
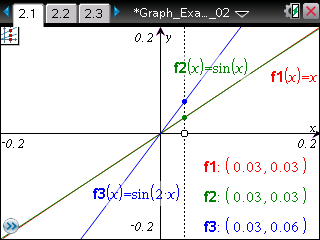
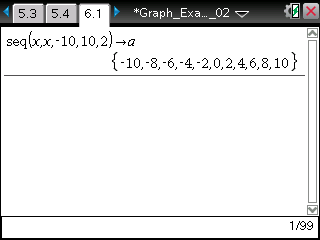
原点に近いところでは，y＝xとy＝sin xは同じような値を，y＝sin 2xは2倍の値をとっています。

代数的に解いていることをグラフで見て納得です。

　TI-Nspire CX

代数的に解く前に視覚的に考えてみましょう。問題の関数のグラフを描いてみましょう。そこから，おのずと答えも見えてきます。仮に計算間違いをしても気づきます。

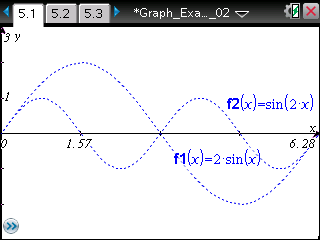
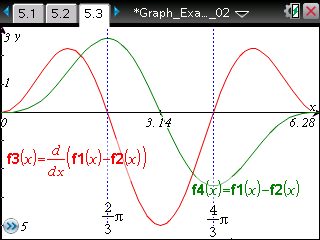
２つの三角関数を足してできる関数の周期は？ 掛けてできる関数の周期は？周期とグラフの対称性についても視覚的に確認し理解しましょう。